An attractor is the set of states a System tends to be in given what it is or how it can maintain its boundaries. An attractor defines a stable system; a system’s possible attractors can be more abstractly represented in an Attractor Landscape.
In mathematical terms,
[a]n attractor is a set of states (points in the phase space) … towards which neighboring states in a given basin of attraction asymptotically approach in the course of dynamic evolution. An attractor is defined as the smallest unit which cannot be itself decomposed into two or more attractors with distinct basins of attraction. This restriction is necessary since a Dynamical System may have multiple attractors, each with its own basin of attraction.Weisstein
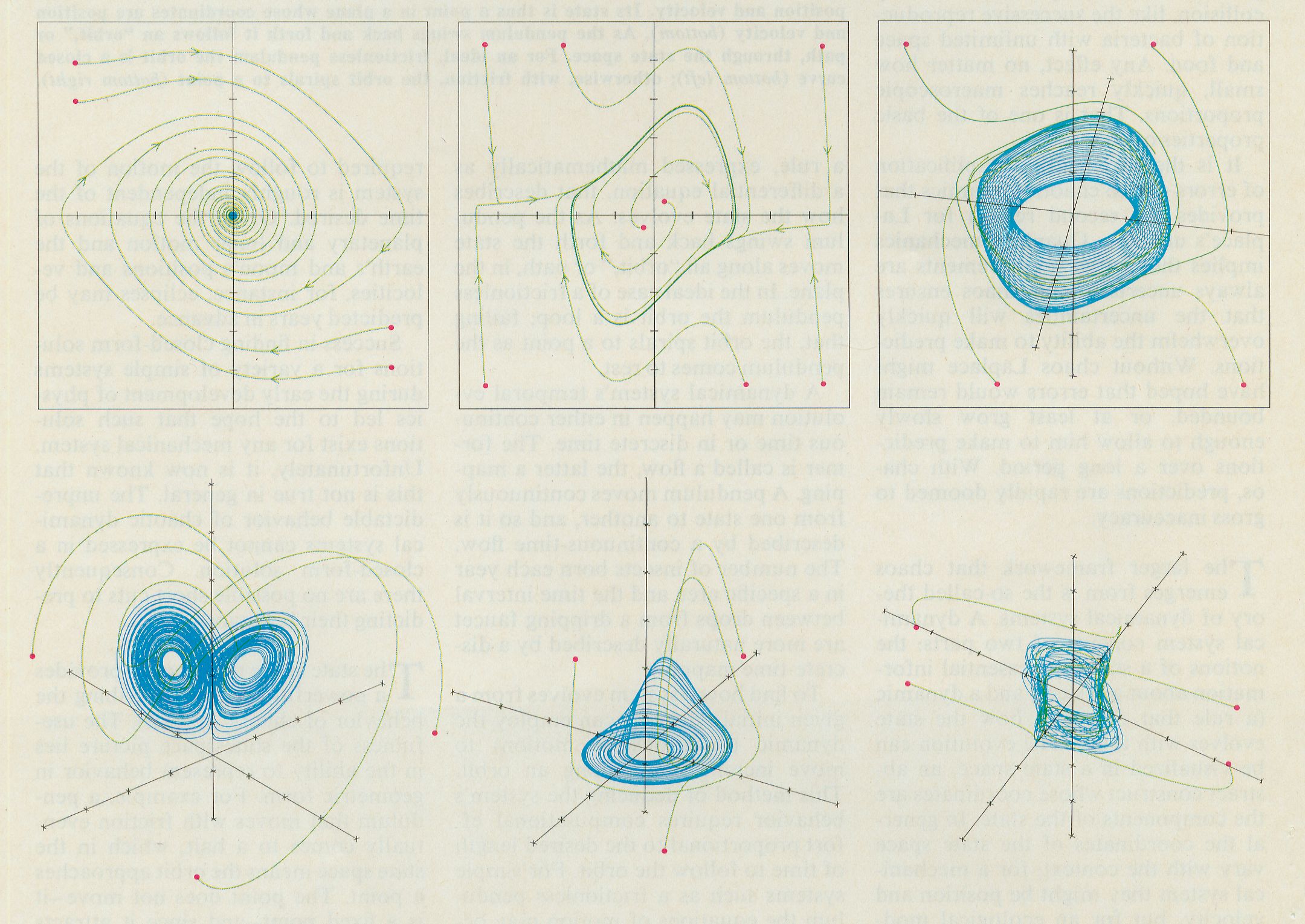
This means that an attractor’s states are never actualised themselves, but the system tends to be in states as close as possible to them. Keeping this in mind, we can adopt the slightly looser formulation of a system being in an attractor state as actually meaning “in a state very nearby”, i.e. in the region around the attractor itself.
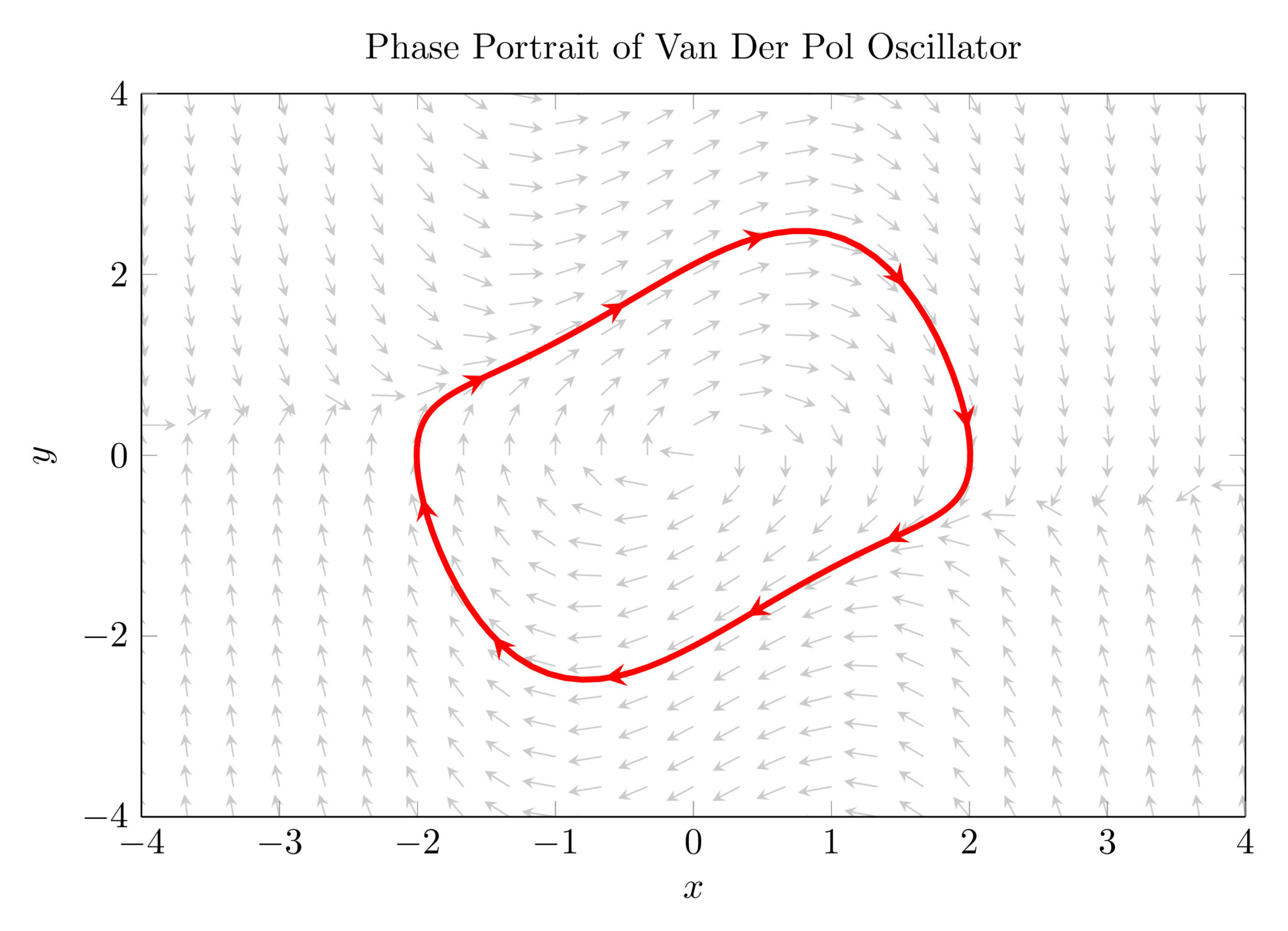
The system’s “movement” towards its attractor states can be described as a gradient flow in the state space’s vector field, i.e. as a continuous succession of states which takes the “shortest way” or “steepest descent” to an attractor.
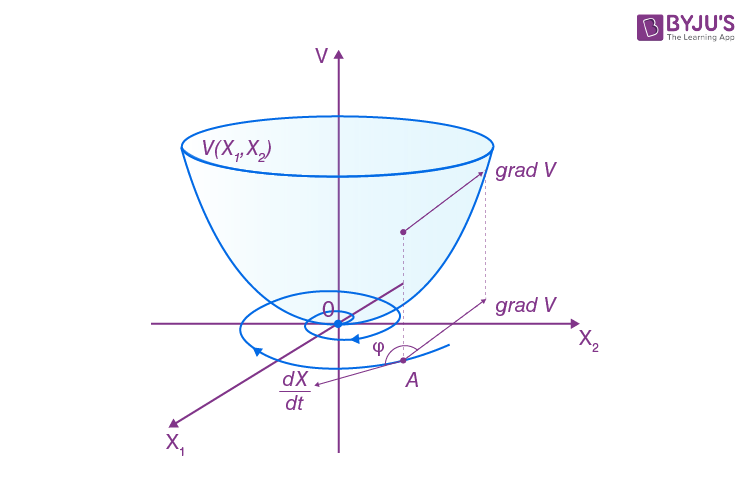
The evolution function describing these gradient flows is the Lyapunov function:
The way something moves through this space depends on its Lyapunov function. This is a mathematical quantity that describes how a system is likely to behave under specific conditions. It returns the probability of being in any particular state as a function of that state (or, put differently, as a function of the system’s position in the state space …). If we know the Lyapunov function for each state of the system, we can write down its flow from one state to the next – and so characterise the existence of the whole system in terms of that flow.Friston (2017)
The gradient flows can be decomposed into fluctuation and
oscillation, the system-specific composition of which
determines the type of attractor the flows correspond to and the
kind of system they describe:Friston (2019). Notice how this classification and
description resonates with Dave Snowden’s Cynefin
Framework.
- Chaotic systems: unordered systems in Thermal Equilibrium, prevalent at very small scales. Their flows have no attractors, i.e. are pure fluctuation. An example are quantum systems.
- Rigid systems: ordered systems in equilibrium steady states with simple attractors (e.g. limit cycles), mostly found at large scales. Their flows are pure oscillation, which (in real systems) over time decays into a fixed end state – or chaos. Examples are the classic pendulum and our solar system.
- Complex Systems: itinerant systems in Non-equilibrium Steady States with strange attractors, i.e. systems that always visit states that are very similar to each other, but never the same. Mostly found at mid scales. An example are biological systems.
We are interested in systems that are, have been, or could be stable, so the last category is of special importance to us.
References
- Abraham & Shaw (1992): Dynamics: The Geometry of Behavior
- Friston (2017): “The mathematics of mind-time”
- Friston (2019): “A free energy principle for a particular physics”
- Weisstein: “Attractor”